Visualizing Precession in Schwarzschild Spacetime¶
Importing required modules¶
[10]:
import numpy as np
from einsteinpy.geodesic import Timelike
from einsteinpy.plotting.geodesic import StaticGeodesicPlotter
Setting up the system¶
Initial position & momentum of the test partcle
Spin of the Schwarzschild Black Hole (= 0)
Other solver parameters
Note that, we are working in M-Units (\(G = c = M = 1\)). Also, since the Schwarzschild spacetime has spherical symmetry, the values of the angular components do not affect the end result (We can always rotate our coordinate system to bring the geodesic in the equatorial plane). Hence, we set \(\theta = \pi / 2\) (equatorial plane), with initial \(p_\theta = 0\), which implies, that the geodesic should stay in the equatorial plane.
[11]:
position = [40., np.pi / 2, 0.]
momentum = [0., 0., 3.83405]
a = 0.
steps = 5500
delta = 1.
Calculating the geodesic¶
[12]:
geod = Timelike(
metric="Schwarzschild",
metric_params=(a,),
position=position,
momentum=momentum,
steps=steps,
delta=delta,
return_cartesian=True
)
Plotting the geodesic¶
[13]:
sgpl = StaticGeodesicPlotter()
sgpl.plot(geod)
sgpl.show()
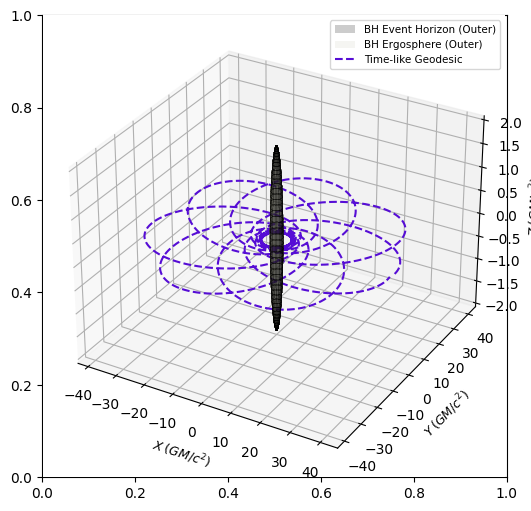
Apsidal Precession is easily observed through the plot, above, and as expected, the geodesic is confined to the equatorial plane. We can visualize this better, with a few 2D plots.
[5]:
sgpl.clear()
sgpl.plot2D(geod, coordinates=(1, 2)) # Plot X & Y
sgpl.show()
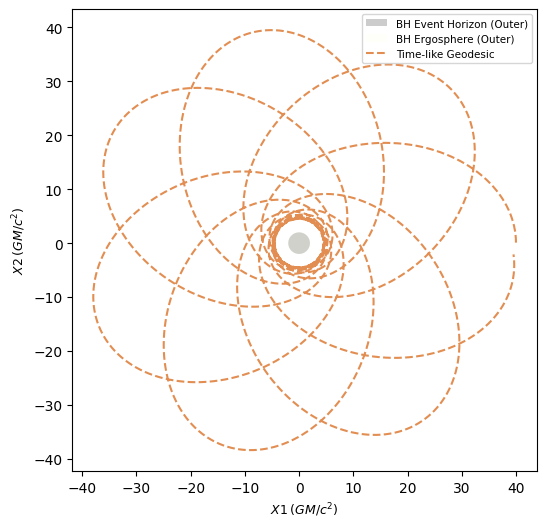
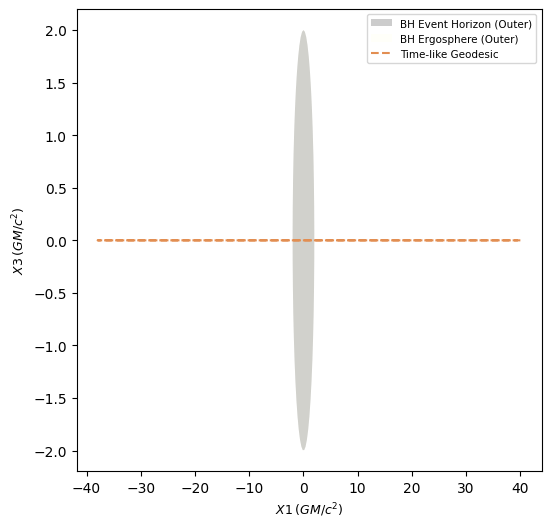
[16]:
sgpl.clear()
sgpl.plot2D(geod, coordinates=(1, 3)) # Plot X & Z
sgpl.show()
[17]:
sgpl.clear()
sgpl.plot2D(geod, coordinates=(2, 3)) # Plot Y & Z
sgpl.show()
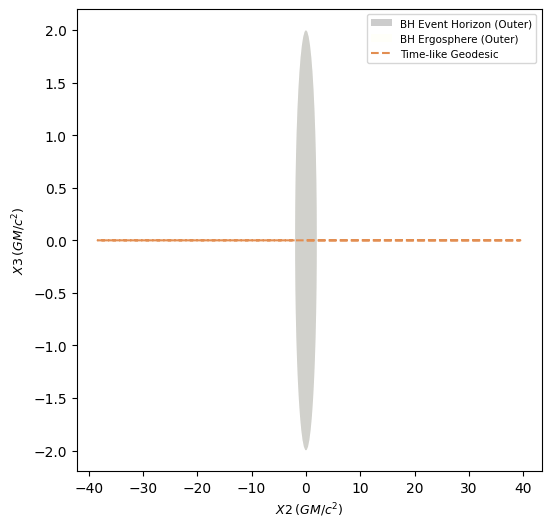
Let’s see, how the coordinates change, with \(\lambda\) (Affine Parameter).
[18]:
sgpl.clear()
sgpl.parametric_plot(geod, colors=("cyan", "magenta", "lime")) # Plot X, Y, Z vs Lambda (Affine Parameter)
sgpl.show()
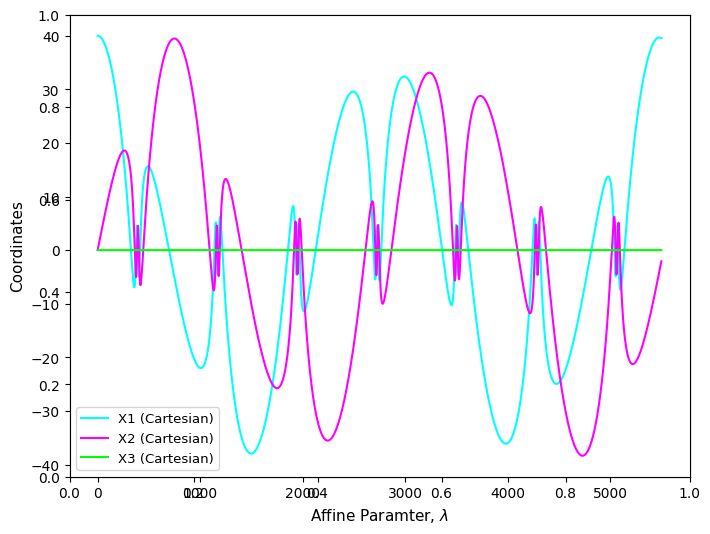
The lag between \(X1\) (\(x\)-component) and \(X2\) (\(y\)-component), in the parametric plot, reaffirms the results from above. Also, \(X3 \approx 0\) (\(z\)-component) in this plot, which is expected, as the geodesic never leaves the equatorial plane.